Wolfram Language allows creation of computational 3D models. These are different from those you can build with your own hands such as SketchUp etc, because computations are often intrinsically different from the way humans see and think. Let’s take for example Calabi-Yau Surface. It is a mathematical object and it is hard to imagine it. […]
Posts Categorized: Demonstrations Project
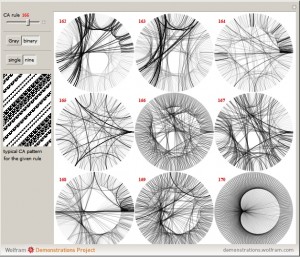
Iconography for Elementary Cellular Automata Based on Radial Convergence Diagrams
My recent publication at the Wolfram Demonstrations Project: “Iconography for Elementary Cellular Automata Based on Radial Convergence Diagrams“. Consider a complete set of initial conditions for a finite elementary cellular automaton (ECA). This set can be indexed by integers using a Gray code or a binary to decimal conversion. During the ECA evolution, the […]
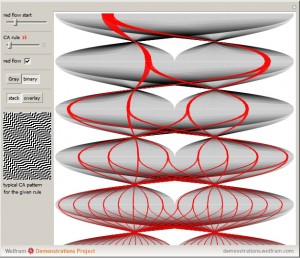
Order, Chaos, and the Formation of a Cantor Set Attractor in Elementary Cellular Automata
My recent publication at the Wolfram Demonstrations Project: Order, Chaos, and the Formation of a Cantor Set Attractor in Elementary Cellular Automata Consider finite elementary cellular automata (ECA) of size 10. All possible binary vectors of length 10 form a complete set of initial conditions (CSIC). Every step of an ECA evolution maps this set to […]
Time Series and Cobwebs for Arbitrary Recursive Maps on the Unit Interval
My new publication at the Wolfram Demonstration Project is Time Series and Cobwebs for Arbitrary Recursive Maps on the Unit Interval. Follow the link to view interactive version. Here is an exert from text: “The logistic map is probably the most famous and simplest example of a function from the unit interval onto itself that […]
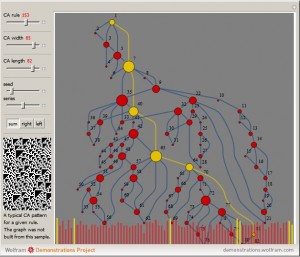
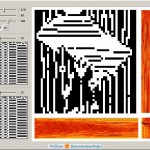
Horizontal Visibility Graphs for Elementary Cellular Automata
My new publication at the Wolfram Demonstration Project is Horizontal Visibility Graphs for Elementary Cellular Automata. Follow the link to view interactive version. Here is an exert from text: “A time series can be formed from an evolution of a finite elementary cellular automaton (ECA). This can be done in a few different ways. We can […]
Lissajous Patterns on a Sphere Surface
Another Demonstration of mine was published at the Wolfram Demonstration Project. It helps to explore and create spherical artistic designs. I generalized Lissajous curves to spherical coordinates. Azimuthal and polar angles undergo oscillations while the radius is kept constant. Although with the parameterization given I sought to emphasize the artistic side of Lissajous patterns, other spherical parameterizations […]
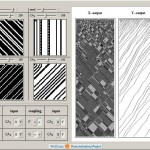
Voronoi Image of Random Walks
The Wolfram Demonstration Project has an excellent example by Yu-Sung Chang showing construction of a Voronoi diagram using distance transform on a set of points in 2D plane. Here same method is used on a set of points which perform random walks. All calculations and animation are done in Mathematica. Yu-Sung Chang Demonstration: demonstrations.wolfram.com/VoronoiImage/ Voronoi Image […]
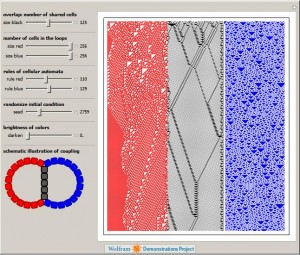
Cellular Automata Coupled by Overlap or Common Boundary
Another short code I wrote in Mathematica language was accepted by The Wolfram Demonstrations Project. The Demonstration shows the evolution of two elementary cellular automata (CA) sharing several cells. CA are often treated as isolated systems with simple cyclic or Dirichlet boundary conditions. Realistic systems, in contrast, interact with the environment through a boundary. Boundaries […]
Two-Dimensional Cellular Automata from One-Dimensional Rules
The Wolfram Demonstrations Project published my program which shows how to reproduce some two-dimensional (2D) cellular automata (CA) with one-dimensional (1D) rules. Thus a large subclass of 2D CA can be conveniently labeled through the standard Wolfram indexing of 1D CA. One step of time evolution of a 2D CA is obtained in two stages. […]
Coupled Cellular Automata: Symbiotic Patterns and Synchronization
Trivial systems with primitive standalone behavior can produce rich dynamics working in collaboration. The Wolfram Demonstrations Project published my program which allows to couple up to four different one-dimensional elementary cellular automata. It produces some interesting patterns and behaviors beyond those of standalone cellular automata. The program is basically applies idea of coupled recursive maps […]
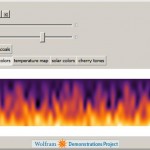
Simulating Flickering Fire with Noisy Cellular Automaton
This is another Mathematica program I wrote published by the Wolfram Demonstrations Project. The program animates flickering fire with a simple mathematical algorithm using Wolfram rule-99 cellular automaton. The algorithm is based on calculation of eigenvalues of a matrix representing the cellular automaton evolution. To play with this program and to read more detailed explanation […]
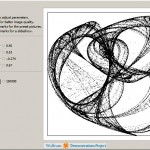
Peter de Jong Attractors
The Wolfram Demonstrations Project published a program I wrote in Mathematica code that visualizes recursive formula attributed to Peter de Jong: It can produce beautiful nontrivial structures called attractors. Click on the picture to go to the Wolfram demonstration page where you can animate and interact with this program.