An article I wrote for Wolfram Blog was just released. Here is the beginning: “On early Monday morning I noticed an interesting question posted on Mathematica Stack Exchange titled quite innocently “xkcd-style graphs.” Due to the popularity of Randall Munroe’sxkcd web comic, I expected a bit more than average of about ten or so up-votes, a few bookmarks. Little did I […]
Posts Categorized: Wolfram
Polyhedra obtained by stellation
Stellation is the process of constructing polyhedra by extending the facial planes past the polyhedron edges of a given polyhedron until they intersect. The set of all possible polyhedron edges of the stellations can be obtained by finding all intersections on the facial planes. Since the number and variety of intersections can become unmanageable for […]
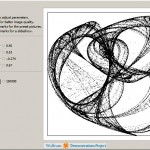
Lissajous Patterns on a Sphere Surface
Another Demonstration of mine was published at the Wolfram Demonstration Project. It helps to explore and create spherical artistic designs. I generalized Lissajous curves to spherical coordinates. Azimuthal and polar angles undergo oscillations while the radius is kept constant. Although with the parameterization given I sought to emphasize the artistic side of Lissajous patterns, other spherical parameterizations […]
Stereoscopic 3D Macromolecule 1TF6
Stereoscopic 3D Macromolecule 1TF6 from Vitaliy Kaurov on Vimeo. To watch this video you need “red-cyan anaglyph glasses”. This video was made with Mathematica 7. This type of red-cyan anaglyph videos can be useful for display of complex 3D structures. Once the structure is built it takes just a few lines of Mathematica code to […]
Peter de Jong Ephemeral Attractors
I made another video with Mathematica. The six changing shapes in the video are called attractors. They are graphical forms of a simple mathematical formula attributed to Peter de Jong. At any given moment the way a single attractor looks depends only on four numbers. A slight variation in these numbers can remarkably change the […]
“Mathematica Render” channel and group on Vimeo
“Mathematica Render” channel and group were recently created on Vimeo to gather a community of enthusiasts designing videos using Wolfram Research Mathematica software. The goal is to promote Mathematica examples of dynamic visualizations that can be used in research, education and art. With such Mathematica capabilities as simulated camera, lighting, image processing, various export options, […]
Voronoi Image of Random Walks
The Wolfram Demonstration Project has an excellent example by Yu-Sung Chang showing construction of a Voronoi diagram using distance transform on a set of points in 2D plane. Here same method is used on a set of points which perform random walks. All calculations and animation are done in Mathematica. Yu-Sung Chang Demonstration: demonstrations.wolfram.com/VoronoiImage/ Voronoi Image […]
Wolfram|Alpha Launches Widgets
Wolfram Alpha LCC launched Widgets and Widget Builder on July 27, 2010. Users are now able to incorporate customizable Wolfram|Alpha queries into their websites, blogs, and social networking sites. Because of the simplicity and power of Widgets, the implications are quite remarkable. Anyone can design an app with personally customized data and calculation interface and […]
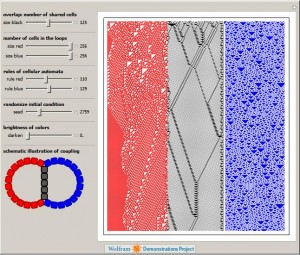
Cellular Automata Coupled by Overlap or Common Boundary
Another short code I wrote in Mathematica language was accepted by The Wolfram Demonstrations Project. The Demonstration shows the evolution of two elementary cellular automata (CA) sharing several cells. CA are often treated as isolated systems with simple cyclic or Dirichlet boundary conditions. Realistic systems, in contrast, interact with the environment through a boundary. Boundaries […]
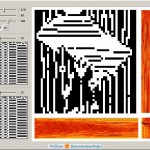
Two-Dimensional Cellular Automata from One-Dimensional Rules
The Wolfram Demonstrations Project published my program which shows how to reproduce some two-dimensional (2D) cellular automata (CA) with one-dimensional (1D) rules. Thus a large subclass of 2D CA can be conveniently labeled through the standard Wolfram indexing of 1D CA. One step of time evolution of a 2D CA is obtained in two stages. […]
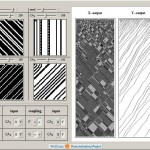
Coupled Cellular Automata: Symbiotic Patterns and Synchronization
Trivial systems with primitive standalone behavior can produce rich dynamics working in collaboration. The Wolfram Demonstrations Project published my program which allows to couple up to four different one-dimensional elementary cellular automata. It produces some interesting patterns and behaviors beyond those of standalone cellular automata. The program is basically applies idea of coupled recursive maps […]
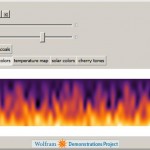
Simulating Flickering Fire with Noisy Cellular Automaton
This is another Mathematica program I wrote published by the Wolfram Demonstrations Project. The program animates flickering fire with a simple mathematical algorithm using Wolfram rule-99 cellular automaton. The algorithm is based on calculation of eigenvalues of a matrix representing the cellular automaton evolution. To play with this program and to read more detailed explanation […]
Peter de Jong Attractors
The Wolfram Demonstrations Project published a program I wrote in Mathematica code that visualizes recursive formula attributed to Peter de Jong: It can produce beautiful nontrivial structures called attractors. Click on the picture to go to the Wolfram demonstration page where you can animate and interact with this program.